Вычислите:

Ответ запишите в виде десятичной дроби. При необходимости округлите до десятых.

В качестве разделителя можете использовать точку или запятую.

Ответ: 22,5

Решение. Рассмотрим две дроби вида для некоторого x ≠ 0 и найдем их сумму:

Перестановкой называется упорядоченный набор без повторений чисел 1, 2, … n, обычно трактуемый как биекция на множестве 1, 2, … n, которая числу i ставит в соответствие i-й элемент из набора (обозначается как σ(i)). Число n при этом называется длиной перестановки. Множество всех перестановок длины n обозначается как Sn. Инверсией перестановки σ ∈ Sn называется пара (i, j), i, j, ∈ такая, что i < j, но σ(i) > σ(j).

Найдите суммарное число инверсий у всех перестановок из S10

Где i (σ) — число инверсий перестановки σ. В качестве ответа введите натуральное

число.

Ответ: 81648000

Решение. Нам нужно посчитать количество троек вида (i, j, σ), где σ ∈ Sn и (i, j) — инверсия перестановки σ. Количество способов выбрать i и j равно.

При фиксированных i и j можно выбрать значения σ(i) и σ(j) такжеспособами. Итого для фиксированных i, j, σ(i) и σ(j) мы можем (n − 2)! способами выбрать значения для всех σ(k), k ≠ i, j. Таким образом,

Маша каждый день после работы собирается пойти на спорт. Известно, что она так и

не сходит на спорт на неделе с вероятностью 1/3, а с вероятностью 2/3 сходит, но только в один из будних дней, причем в любой с равной вероятностью. В пятницу утром Аня заметила, что Маша так и не сходила на спорт на этой неделе. Какова вероятность того, что в пятницу она сходит на спорт? В качестве ответа введите несократимую дробь, например ½.

Ответ: 2/7

Решение. Пусть событие A — это то, что Маша сходит на спорт, а событие B — то, что она не появится на спорте с понедельника по четверг. Надо найти P (A|B), что по формуле Байеса равняется , так как, если мы знаем, что Маша сходила на спорт, но не сходила с понедельника по четверг, это значит, что она пошла на спорт в пятницу с вероятностьюпо условию. , так как Маша не сходит на спорт с понедельника по четверг, либо если не пойдет на спорт вообще, либо, если пойдет, то в пятницу.

Решите в целых числах уравнение:

В качестве ответа запишите сумму всех решений.

Ответ: 24

Решение. Домножим на два и перенесем влево. Прибавим 8 к обеим частям и выделим полные квадраты . Очевидно, что два квадрата из трех должны равняться 4, а один — 0. Перебором находим все решения: (4; 4), (4; 2), (2; 4), (2; 0), (0; 2), (0; 0).

В опенспейсе 25 очень длинных рядов. В одном ряду могут сидеть либо только аналитики, либо только разработчики. Более того, разработчики могут сидеть на одном ряду, только если они не знакомы, а аналитики, наоборот, могут сидеть на одном ряду, только если знакомы.

В опенспейс пришли k команд, в каждой один аналитик и один разработчик. Известно, что разработчики знакомы в том и только в том случае, когда знакомы аналитики из их команд. При каком наибольшем k любые k таких команд заведомо можно разместить по 25 рядам?

Ответ: 24

Решение. Если все команды знакомы друг с другом, разработчикам нужно k рядов, и аналитикам — еще один. Значит, больше 24 нельзя. Почему 24 можно, докажем по индукции. Пусть n команд можно разместить по n + 1 ряду (в базе индукции мы сажаем одну команду на два ряда). Тогда посмотрим на n + 1 команду. Уберем одну команду, оставшиеся распределим на n + 1 ряд по предположению индукции. Пусть команда, которую убрали, пойдет выбирать себе ряд. Аналитик не хочет сидеть на одном ряду с незнакомыми ему аналитиками из m команд, а разработчик — со знакомыми ему n − m разработчиками. Значит, им может не понравиться не более n рядов, а следовательно, на какой-то ряд кто-то из них может сесть. Второй занимает n + 2-й ряд.

Дарина сказала четырем аналитикам по числу так, чтобы остальные не слышали. После этого она сообщила: «Я сказала вам четыре разных числа. Это последовательные двузначные натуральные числа, одно из которых делится на 8, а другое — на 7. Может ли каждый из вас назвать все четыре числа, которые я вам сказала?» Аналитики подумали и одновременно ответили: «Да». Каким может быть наименьшее из чисел, которые Дарина сказала аналитикам? Если ответов несколько, введите в качестве ответа их произведение.

Ответ: 4553472

Решение. Если кратные 7 и 8 числа стоят рядом или через один, получивший это число аналитик не может с уверенностью сказать, какое число у каждого из его коллег. Например, если аналитик получает число 14, он понимает, что у двух его коллег числа 15 и 16, но не знает число оставшегося. Оно может равняться 13 или 17. Значит, между кратными 7 и 8 числами должно быть еще два числа, тогда всю четверку можно определить однозначно. Подходят четыре четверки: (21,22,23,24); (32,33,34,35); (77,78,79,80); (88,89,90,91).

Саньцзегунь — китайский трехсекционный боевой цеп. Представляет собой три последовательно соединенные веревкой или цепью деревянные (реже металлические) палки. Аня взяла саньцзегунь, состоящий из трех палок одинакового размера, и бросила его на землю.

Какова вероятность того, что крайние палки пересекаются? Считайте, что саньцзегунь представляет собой ломаную из трех звеньев, а всевозможные углы, которые могут образовать крайние звенья со средним, равновероятны. В качестве ответа введите несократимую дробь, например ½.

Ответ: 1/12

Решение. Ломаную, образованную палками, назовем ABCD. Пусть α = ∠ABC — угол между первой и второй палкой, а β = ∠BCD — угол между второй и третьей палкой. Можно считать, что 0 ≤ α ≤ π, и тогда 0 ≤ β ≤ 2π. Элементарными исходами являются пары (α; β). На координатной плоскости αOβ они заполняют прямоугольник G.

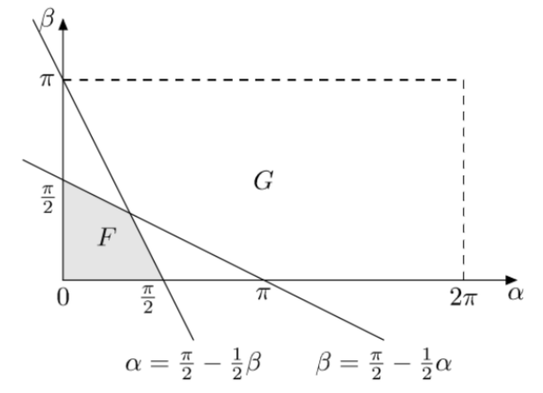
Первая и третья палка AB и CD пересекаются в некоторой точке K, только если луч

CD лежит внутри угла BCA, а луч BA лежит внутри угла CBD, то есть 0 ≤ ∠BCD <

∠BCA, 0 ≤ ∠ABC < ∠CBD. Учитывая, что треугольники ABC и BCD равнобедренные,

получаем два симметричных условия . На координатной плоскости αOβ эти неравенства определяют четырехугольник F внутри прямоугольника G. Искомая вероятность равна отношению площадей четырехугольника F и прямоугольника G, то есть 1/12.

В команде Т‑Банка произошла реорганизация — объединились два отдела. Новые коллеги хотят сидеть рядом, поэтому офису требуется ремонт. Прежние места каждого отдела имели форму прямоугольника. Новая площадка должна быть квадратной, а также содержать предыдущие места: некоторые разработчики очень привязаны к ним. К сожалению, размеры офиса ограниченны, поэтому зона должна иметь минимальную площадь. Строители пытаются посчитать, сколько материала им понадобится для ремонта. Для этого им нужно знать итоговую площадь обновленной площадки. Пожалуйста, помогите им.

Решение

Чтобы покрыть оба прямоугольника, нужно покрыть все точки с x-координатой из отрезка [xmin; xmax], где xmin — минимальная x-координата среди всех вершин прямоугольников. То же верно и для y-координаты. Значит, новая зона должна покрывать прямоугольник [xmin; xmax] × [ymin; ymax]. Чтобы покрыть такой прямоугольник квадратом, достаточно взять сторону квадрата равной наибольшей стороне этого прямоугольника.

Аня — координатор стажировок в Т‑Банке. Она хочет нанять самых сильных олимпиадников. Чтобы понять, кто лучший, Аня решила проанализировать результаты командной олимпиады за последние N лет. Она знает все команды, занявшие первое место. Каждая команда задается тройкой имен, причем их порядок не важен, то есть записи ANTON BORIS CHRIS и BORIS ANTON CHRIS задают одну и ту же команду. Ане нужны лучшие из лучших, поэтому она хочет знать, какое максимальное число раз побеждала команда в одном и том же составе. Вы дружите с Аней, поэтому согласились ей помочь.

Решение

Для начала отсортируем каждую команду лексикографически, так как порядок членов команды не имеет значения для состава. Теперь для каждой команды можно пробежаться по всем остальным и сравнить составы, а при совпадении увеличивать счетчик вхождения текущей команды. После подсчета промежуточного ответа нужно проверить, больше ли он глобального ответа на задачу. Это решение имеет квадратичную асимптотику, что укладывается в ограничения.

Один из ваших знакомых стал стажером-аналитиком в команде Т‑Банка. У него есть данные за n дней о том, как клиенты подключают и отменяют подписки на один из сервисов. По странному стечению обстоятельств дни чередуются: в первый день подписки только подключались, во второй только отменялись и так далее, то есть каждый день число приобретенных подписок составляет  — число подключенных или отключенных подписок за i-й день.

Во время анализа данных ваш знакомый задался вопросом, увеличилась бы прибыль компании, если бы данные за какие-то дни поменялись местами. В качестве первого этапа он решил поменять местами не более двух дней.

Проверьте, сможете ли вы стать стажером-аналитиком в Т‑Банке. Для этого предлагаем вам посчитать максимально возможное значение прибыли, которую можно получить, поменяв местами данные не более чем за два дня. Стоимость одной подписки можно считать равной 1.

Решение

Рассмотрим вклад чисел, которые стоят на четных и нечетных местах. Заметим, что для увеличения максимальной прибыли нужно заменить максимальное число с четным индексом (отмененные подписки) на минимальное число с четным индексом (подключенные подписки). Менять нужно только в том случае, если оно не ухудшает итоговый результат (именно поэтому можно вообще не делать обменов).

Докажем, почему всегда выгодно так делать. Для начала заметим, что менять числа на местах с одинаковой четностью нет смысла, так как общий результат суммирования прибыли никак не изменится. Далее предположим, что в оптимальном решении меняются числа с индексами i и j, а в нашем — c индексами k и l, причем i и k нечетные, а j и l четные. Тогда, если вместо ai менять ak, мы улучшим оптимальный ответ на + ai — ak, что ≥ 0, так как элемент на позиции k — минимальный среди стоящих на нечетном месте. То же верно и для другой пары индексов: если менять не j-й элемент, а l-й, ответ увеличится на + ai — aj, что ≥ 0, так как al — максимальный среди стоящих на четном месте. Следовательно, наше решение не хуже, чем оптимальное, то есть является таковым.

Вы прошли на стажировку и получили свое первое задание. Ваш куратор попросил прочитать и обработать файл конфигурации, состоящий из строк трех типов:

• { — начало блока;
• } — конец блока;
• variable =< value > — присваивание в переменную с именем variable

значения value.

value может быть двух типов:

• число, по модулю не превосходящее 109;
• название переменной, чье значение нужно присвоить.

В файле нет пробелов и каждая операция записана в отдельной строке. Имена всех переменных состоят не более чем из 10 строчных латинских букв (a, . . . , z). Изначально все переменные имеют значение 0. Как только встречается выражение присваивания, необходимо сразу же его выполнить. Это значение сохраняется до конца блока (если не будет перезаписано), и после конца блока возвращается старое значение переменной.

Куратор хочет проверить, насколько хорошо вы анализируете код, поэтому попросил вас вывести значение переменной variable1 после каждого присваивания вида variable1 = variable2.

Решение

Будем читать файл построчно и поддерживать для каждой переменной тот стек значения, который был присвоен. Кроме того, для каждого уровня вложенности блоков будем поддерживать множество переменных, которые были изменены на этом уровне.

При каждом новом присваивании нужно посмотреть, менялось ли уже значение этой переменной в этом блоке. Если нет, нужно добавить на стек новое значение, а если да — перезаписать его. При выходе из блока для всех переменных, которые были на нем изменены, нужно убрать последнее присвоенное значение, то есть последнее число из стека для этой переменной.

При таких операциях мы всегда сможем узнать текущее значение переменной, посмотрев на вершину стека.

Пройдя тестовое задание от куратора из предыдущей задачи, вы получили новое. На этот раз вам нужно улучшить систему поиска карточек в бухгалтерии Т‑Банк.

Всего у нас работает n людей. Каждый человек определяется своей фамилией, состоящей из строчных букв латинского алфавита (a, . . . , z). К сожалению, бумажные записи со временем становятся нечитаемыми, так как конец фамилии стирается. Но команда бухгалтерии отлично знает систему хранения карточек и умеет находить любого сотрудника по префиксу его фамилии.

Для более быстрой работы дополнительно требуется знать k-го в лексикографическом порядке человека среди всех с заданным префиксом. Задачу по быстрому поиску такого человека и поставил перед вами куратор.

Решение

Отсортируем все фамилии. После этого для ответа на запрос нужно искать k-е слово с подходящим префиксом. Например, это можно сделать при помощи линейного прохода, но тогда бы решение работало за , что не укладывается в ограничения по времени — всего нужно сделать q запросов.

Так как все фамилии с подходящим префиксом после сортировки лежат подряд, для ускорения решения можно воспользоваться бинпоиском для нахождения первого слова с заданным префиксом. Далее необходимо посмотреть на (found + ki)-е слово в отсортированном порядке и проверить, что оно подходит, то есть имеет заданный префикс. Это решение тратит на запрос — это удовлетворяет ограничениям.

В офисе Т‑Банка есть несколько лифтов для минимизации времени ожидания и ускорения перемещения по зданию. У лифтов есть особенность: i-й лифт едет только с этажа si до этажа fi без промежуточных остановок. По задумке строителей, лифты везут пассажиров только вверх (вниз все ходят по лестницам).

В первый день стажировки вы решили прокатиться на максимальном числе лифтов подряд, составив цепь. Цепью вы называете последовательность лифтов, для которых для любых двух лифтов, имеющих в цепи номера i и i + 1, выполняется условие fi = si+1, то есть между двумя лифтами вам не нужно пользоваться лестницей, чтобы добраться от одного до другого. Определите максимально возможную длину цепи лифтов, на которых вам удастся прокатиться.

Решение

Будем решать эту задачу с помощью динамического программирования. Отсортируем лифты по возрастанию их конечного этажа. Посчитаем динамику dpk — максимальную длину цепочки, позволяющей доехать до k-о этажа. Рассмотрим i-й лифт. Если мы возьмем его в ответ, то для получения цепочки предыдущий лифт должен иметь конечный этаж, равный стартовому для i-о лифта. Значит, надо пробовать улучшать ответ для высоты ri ответом для высоты . Динамика будет считаться правильно из-за сортировки лифтов по возрастанию конечного этажа.

Заметим, что из-за ограничений на высоту лифтов (они могут быть до 109) перед подсчетом значения стартового и конечного этажей необходимо сжать или воспользоваться map.

После работы ваш коллега, стажер Павел, решил зайти в магазин. Как и вы, Павел — разработчик, поэтому каждое свое действие он выполняет по алгоритму в строгой последовательности.

Супермаркет для Павла — прямая с полками. На каждой полке стоят товары одной категории, а каждая полка помечена какой-то строчной буквой латинского алфавита (a, . . . , z), то есть весь супермаркет можно представлять как строку s.

Павел хочет взять по одному товару с каждой полки в каком-то порядке. Для этого ему нужно сделать две операции:

• Взять товар с текущей полки и положить в корзину, если он не сделал этого ранее.
• Передвинуться к следующей полке. Если он стоял у последней полки, то возвращается к первой.

Павел любит порядок и хочет складывать товары в отсортированном порядке, а именно: сначала он хочет взять по одному товару с полок с буквой a, если они есть, затем с буквой b и так далее до z. У Павла был тяжелый день, и он хочет домой, поэтому планирует закончить с покупками как можно быстрее. Для этого он решил брать товары не со всех полок, а только с какого-то подотрезка, то есть рассматривать все полки с l-й по r-ю.

Пожалуйста, помогите Павлу быстрее попасть домой и посчитайте, сколько передвижений (операций второго типа) ему нужно будет сделать.

Решение

Для начала рассмотрим медленное решение задачи. Для каждого запроса будем поддерживать двумерный вектор, где для каждой буквы будут записаны все ее вхождения. Дальше остается смоделировать движение Павла: для первой буквы нужно в отсортированном порядке пройти все буквы, а для всех следующих нужно сначала найти ближайшую справа букву.

Полученное решение работает за на запрос. При числе запросов и длине супермаркета до 105 такое решение не укладывается во временные ограничения.

Для ускорения заметим, что для каждой буквы нас интересуют не все ее вхождения, а только последнее на подотрезке и последнее слева от текущей позиции Павла.

Пояснение: если у нас нет буквы слева от Павла, достаточно дойти до последнего вхождения на подотрезке. Иначе нужно идти до его конца, а потом возвращаться до этого вхождения. Необходимые позиции можно поддерживать при помощи массива предыдущих букв prev[position][letter], причем его достаточно посчитать в начале, а дальше только использовать. В итоге получаем на предподсчет и  на запрос.

В Т‑Банке решили освоить новую нишу, а именно: открыть внутренний стартап по продаже доменов. Каждый домен представляет собой строку, состоящую только из букв S, T, A, R.

Каждому покупателю хочется не просто продать строку, а продать нужную строку. Пусть у каждого покупателя есть строки P и Q. Тогда ему подходят только строки, у которых первые |P| символов совпадают с P и последние |Q| символов совпадают с Q.

Для начала было закуплено n доменов для m покупателей. Теперь нужно понять, хватит ли их для всех покупателей. Чтобы получить ответ на этот вопрос, посчитайте число подходящих для каждого покупателя строк.

Решение

Для начала рассмотрим более простую версию задачи. Предположим, что в запросе был указан только префикс строки. То есть запрос заключается в том, что нам нужно вывести количество строк из словаря, у которых первые Pi символов совпадают с |Pi|. Для решения такой задачи воспользуемся бором. Запишем все Si (домены) и все Pj в бор. Теперь заметим, что утверждение «строка S является префиксом строки T» эквивалентно утверждению «вершина бора x, соответствующая строке S, является предком вершины v, соответствующей строке T». Это легко показать из устройства бора. Получается, наша задача свелась к подсчету количества вершин в поддереве.

Для решения исходной задачи будем пользоваться эйлеровым обходом полученного дерева, а именно: посчитаем времена входа и выхода для каждой вершины, соответствующей какой-либо строке. Тогда каждый запрос покупателя представим в качестве отрезка, а каждую строку из набора — в виде точки (можно, например, сопоставлять время входа). Упрощенная задача заключается в поиске количества точек внутри каждого отрезка.

Те же рассуждения можно проделать для развернутых строк Si и Qj. Тогда исходная задача сводится к поиску количества точек в каждом прямоугольнике. Это можно сделать, например, при помощи многомерного сжатого дерева Фенвика.